You should use spatial nested cross-validation
Back to the basics
Before we understand spatial nested-cross validation we should revise briefly about the concept of bias-variance tradeoff as it’s the foundation. There are already too many good resources on the internet that explain the bias-variance tradeoff, but I will try to explain it in a simple and quick way.
What is bias variance tradeoff and why is it important ?
The bias-variance tradeoff is a fundamental concept in machine learning that deals with finding a balance between model complexity and accuracy. Model with high complexity is more likely to overfit the data (low bias, high variance), whereas a model with low complexity is more likely to underfit the data (high bias, low variance). Since the goal of machine learning is to find a model that can generalise well to new data, finding the optimal balance between bias and variance is essential (e.g., the dotted line in the figure below).
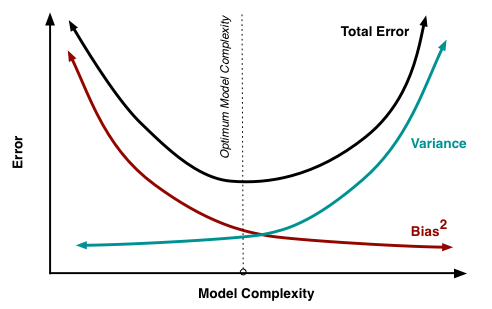
img source: Wikimedia commons
How do we find that balance in bias and variance ?
We tune the hyperparameters of the model to avoid both under and over fitting. Hyperparameters are the parameters that are not learned from the data (in contrary to model parameters that are learnt from the data), but are set by the user. For example, the number of trees in a random forest model or the number of neurons in deep learning models. So tuning the hyperparameters involves finding the optimal values for these parameters. Remember, the objective is to find the optimal model parameter that enables the model to have a broader range of generalisation.
How do we tune the hyperparameters ?
Hyperparameters are tuned by specifying a range of values for each hyperparameter and then training the model on the training set for each combination of hyperparameter values, and then testing with the test set. The model with the best performance is the one with the optimal hyperparameters. How do we do that ? We use a technique called cross-validation.
What is cross-validation?
Cross-validation is the simplest and the most widely used method for evaluating the performance of machine learning models. The technique involves dividing data into two sets - training and testing - and training the model on the former while assessing its performance on the latter. The procedure is repeated several times, using different training and testing sets each time (aka k-folds cross-validation). You can use this method for comparing and selecting a model, as well as for optimising the hyperparameters.
Here is a figure that shows a 4 fold cross-validation process:
But there is a problem with cross-validation, what’s that ?
Using the same cross-validation technique for both model selection and hyperparameter tuning can lead to overfitting. This is because the model is trained and tested on the same data. So, the model will perform well on the test set, but not on new data. We also need a validation set.
Here comes the nested-cross validation to the rescue
Nested cross-validation separates the model selection process from the hyperparameter tuning process. The outer loop is used for model selection, and the inner loop is used for hyperparameter tuning. This way, the model is trained and tested on different data, making the model more generalisable.
Btw, I made these memes. I just learned a way to make them using Bing image create AI and imgflip quickly within 5 minutes.
Ok that’s a bit of reading, let’s come to the main concept of spatial nested cross-validation
Spatial nested cross-validation is just a nested cross-validation but with coordinates. Spatial data often exhibits spatial autocorrelation, which means that nearby locations are more similar than distant locations. This can result in biased model predictions if the model is trained and tested on data that is not spatially independent. That is even if you run a nested cross-validation there would still be bias. Sorry but your high accuracy score without spatial nested-cross validation is not accurate. Spatial nested cross-validation can account for this spatial autocorrelation and produce more accurate estimates of the model performance. I really like this figure from the mlr tutorial on spatial cross-validation. It shows the spatial cross-validation process, and differentiates with non-spatial methods.
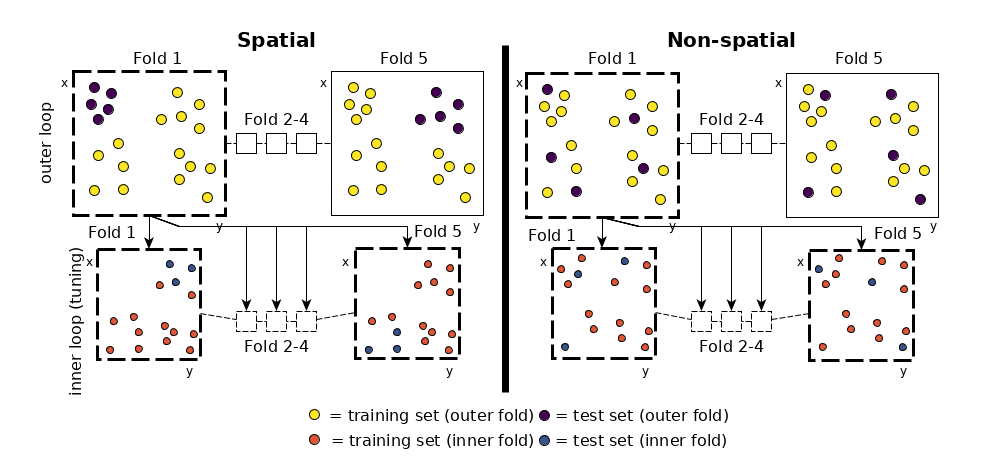img source: mlr tutorial on spatial cross-validation
You see in the figure in the spatial nested cross-validation process, the data is first divided into 5 spatial blocks (the outer folds for testing the model) and within each outer fold is divided into 5 inner folds (i.e., fold 1 is further divided into 5 inner folds) which are used for hyperparameter tuning.
How do you implement spatial nested cross-validation ?
You can manually make spatial folds using the coordinates of the samples, or you can use the mlr3spatiotempcv package in R, which is under the mlr3 suite of packages, and is an awesome package that I have used in two of my research work. Here is a tutorial. Basically, mlr3spatiotempcv leverages other spatial packages like blockCV and sperrorest to make spatial folds.
Perhaps an important decision you have to make is what method to use for making spatial blocks (this is important as it will affect the performance of the model). When the data is distributed well across the study area, then blockCV is the simplest method to use. But if the data is not distributed well, then blockCV is not useful, as some of the testing spatial blocks may just end up having few sampling. In such cases, Clustering methods such as k-nearest neigbor clusters that divides the study areas based on the cluster of the samples is a more appropriate method. You can plot the training, testing, and validation sets to see if they are distributed well across the study area.
Conclusion
Spatial nested cross-validation is an important tool for evaluating and selecting spatial prediction models. It can help produce more accurate predictions, identify the best model parameters, select the best model, and estimate the uncertainty associated with each prediction. Wow, just so little explanation on spatial nested cross-validation. Well, because it’s so simple to understand once you understand what a bias-variance tradeoff is, what cross-validation is, and what nested cross-validation is. But there may be other questions that you might ask:
How many folds to select ?
Typically 5 or 10 folds are used. But it’s a bit more complicated than that. I will cover that in the next blog.
What about different parameter search optimisation process?
This too in the next blog.